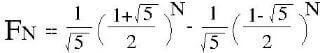费式数列

说明

Fibonacci为1200年代的欧洲数学家，在他的着作中曾经提到：「若有一隻免子每个月生一隻小免子，一个月后小免子也开始生产。起初只有一隻免子，一个月后就有两隻免子，二个月后有三隻免子，三个月后有五隻免子（小免子投入生产）……」。

如果不太理解这个例子的话，举个图就知道了，注意新生的小免子需一个月成长期才会投入生产，类似的道理也可以用于植物的生长，这就是Fibonacci数列，一般习惯称之为费氏数列，例如以下： 1、1 、2、3、5、8、13、21、34、55、89……

解法

依说明，我们可以将费氏数列定义为以下：

fn = fn-1 + fn-2　　if n > 1

fn = n　　　　　　 if n = 0, 1

演算法

费氏阵列的解法很多，基本上可以使用递迴解，演算法最简单，如下：

1
2
3
4
5
6
7
8
9


Procedure FIB(N) [
    IF (N < 0)  
        PRINT ("输入错误"); 

    IF (N = 0 OR N = 1) 
        RETURN (N); 
    ELSE 
        RETURN ( FIB(N-1) + FIB(N-2) ); 
] 

简单，但是不实用，因为太慢了，在求每一个费氏数时，都会发生严重的重覆计算，也就是递迴该行 ( FIB(N-1) + FIB(N-2) )，最差的big-o可以到2的n/2次方，画张递迴的树状图就可以知道重覆计算的数有多少了。

可以採取非递迴的版本，可以将big(o)减至n，演算法如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


Procedure FIB(N) 
    a = 1; 
    b = 1; 
    FOR i = 2 TO N [
        temp = b; 
        b = a + b; 
        a = temp; 
    ]
    RETURN b; 
] 

若想要一次列出所有N之前的费氏数，则可以将for迴圈的部份改以阵列，也就是：

1
2
3
4
5


F(0) = 0; 
F(1) = 1; 
FOR i<-2 TO N [
    F(i) = F(i-1) + F(i-2); 
]

费氏阵列并不是使用递迴来解一定不好，事实上单就执行次数上来说，有一个使用递迴的演算法可以更快 (big(o)是以2为底的Logn值)，但是要使用到乘法运算，所以实际上要看所使用的机器而定。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


Procedure FIB(N) 
    IF (n <= 1)
        RETURN(n); 

    IF (n = 2) 
        RETURN(1); 
    ELSE [ 
        i = n/2; 
        f1 = FIB(i+1); 
        f2 = FIB(i); 

        IF (n mod 2 = 0)
            RETURN( f2*(2*f1-f2) ); 
        ELSE 
            RETURN ( f1**2+f2**2 ); 
    ]
] 

您可以实际使用费氏数列来印证演算法中的那两条公式，其中f1**2表示f1的平方；若将递迴的树状图画出来，就像这样：

另外费氏数列还有公式解，导证方式就不提了：

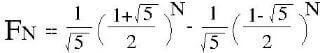
您说，如果免子不只生一隻小免子的话怎麽办？像这种问题，我们可以将费氏数列加以扩充，称之为扩充费氏数列：

fn = X * fn-1 + Y * fn-2　　if n > 1

fn = 1　　　　　　　　　 if n = 0, 1

当X、Y等于1时，自然就是一般的费氏数列了。

想瞭解费氏数列与自然界神奇的关係，可以造访这个网页。

编码参考

C

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


#include <stdio.h> 
#include <stdlib.h> 

#define N 20 

int main(void) { 
    int Fib[N] = {0}; 
    int i; 

    Fib[0] = 0; 
    Fib[1] = 1; 

    for(i = 2; i < N; i++) 
        Fib[i] = Fib[i-1] + Fib[i-2]; 

    for(i = 0; i < N; i++) 
        printf("%d ", Fib[i]); 
    printf("\n"); 

    return 0; 
} 

Java

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


public class Fibonacci {
    public static void main(String[] args) {
        int[] fib = new int[20]; 

        fib[0] = 0; 
        fib[1] = 1; 

        for(int i = 2; i < fib.length; i++) 
            fib[i] = fib[i-1] + fib[i-2]; 

        for(int i = 0; i < fib.length; i++) 
            System.out.print(fib[i] + " "); 
        System.out.println();
    }
}