4N魔方阵

说明

与奇数魔术方阵相同，在于求各行、各列与各对角线的和相等，而这次方阵的维度是4的倍数。

解法

先来看看4X4方阵的解法：

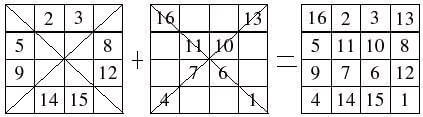
简单的说，就是一个从左上由1依序开始填，但遇对角线不填，另一个由左上由16开始填，但只填在对角线，再将两个合起来就是解答了；如果N大于2，则以 4X4为单位画对角线：

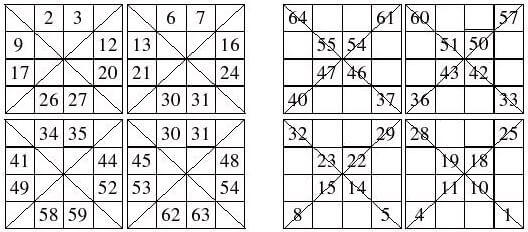
至于对角线的位置该如何判断，有两个公式，有兴趣的可以画图印证看看，如下所示：

左上至右下：j % 4 == i % 4

右上至左下：(j % 4 + i % 4) == 1

参考代码

C

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


#include <stdio.h> 
#include <stdlib.h> 

#define N 8 

int main(void) { 
    int i, j; 
    int square[N+1][N+1] = {0}; 

    for(j = 1; j <= N; j++) { 
        for(i = 1; i <= N; i++){ 
            if(j % 4 == i % 4 || (j % 4 + i % 4) == 1) 
                square[i][j] = (N+1-i) * N -j + 1; 
            else 
                square[i][j] = (i - 1) * N + j; 
        } 
    } 

    for(i = 1; i <= N; i++) { 
        for(j = 1; j <= N; j++) 
            printf("%2d ", square[i][j]); 
        printf("\n"); 
    } 

    return 0; 
}

Java

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


public class Matrix {
    public static int[][] magicFourN(int n) {
        int[][] square = new int[n+1][n+1]; 

        for(int j = 1; j <= n; j++) { 
            for(int i = 1; i <= n; i++){ 
                if(j % 4 == i % 4 || (j % 4 + i % 4) == 1) 
                    square[i][j] = (n+1-i) * n -j + 1; 
                else 
                    square[i][j] = (i - 1) * n + j; 
            } 
        } 
        
        int[][] matrix = new int[n][n];
        
        for(int k = 0; k < matrix.length; k++) {
           for(int l = 0; l < matrix[0].length; l++) {
               matrix[k][l] = square[k+1][l+1];
           }
        }
        
        return matrix;
    }
    
    public static void main(String[] args) {
        int[][] magic = Matrix.magicFourN(8);
        for(int k = 0; k < magic.length; k++) {
            for(int l = 0; l < magic[0].length; l++) {
                System.out.print(magic[k][l] + " ");
            }
            System.out.println();
         }
    }
}